Definition of set:
A set is a collection of well-defined objects.

Explanation of the term “Well-defined”:
Well-defined means, it must be absolutely clear that which object belongs to the set and which does not.
Now, to get basic concepts of sets about the meaning of well-defined the following examples are given below.
1. The collection of vowels in English alphabets. This set contains five elements, namely, a, e, i, o, u.
2. A group of “Singers with ages between 18 years and 25 years” is a set, because the range of ages of the singer is given and so it can easily be decided that which singer is to be included and which is to be excluded. Hence, the objects are well-defined.
3. A collection of “Red flowers” is a set, because every red flowers will be included in this set i.e., the objects of the set are well-defined.
. The collection of past presidents of the United States union is a set.
5. A group of “Young dancers” is not a set, as the range of the ages of young dancers is not given and so it can’t be decided that which dancer is to be considered young i.e., the objects are not well-defined.
6. The collection of cricketers in the world who were out for 99 runs in a test mach is a set.
Thus, basic concepts of sets are explained with the various examples. To know more in details follow the following contents.
Basic Term about set:
Sets: An introduction to sets, methods for defining sets, element of set and use of set notations.
Sets Theory: Brief description on set theory and the important sets used in mathematics.
Objects Form a Set: State, whether the following objects form a set or not by giving reasons.
Elements of a Set: Learn how to find the elements of a set with the help of various types of problems on the basic concepts of sets.
Properties of Sets: Using the basic properties to represent a set learn to solve various basic types of problems on sets.

Representation of a Set: Definition with examples of statement form, roster form or tabular form, set builder form cardinal number of a set and the standard sets of numbers.
Different Notations in Sets: Some of the familiar notations used in sets which are generally required to solve various types of problems on sets.
Standard Sets of Numbers: Learn to represent the standard sets of numbers using the three methods i.e. statement form, roster form and set builder form.
Types of Sets: Definition with examples of empty set or null set, singleton set, finite set, infinite set, cardinal number of a set, equivalent set and equal sets.
Pairs of Sets: Definition with examples of equal set, equivalent set, disjoint sets and overlapping set.
Subset: Definition with examples of subset and its types, super set, proper subset, power set and universal set.
Subsets of a Given Set: How to find the number of subsets of a given set and number of proper subsets of a given set.
Finite Sets and Infinite Sets: Learn how to distinguish between finite set and infinite set with examples.
Power Set: Explanation on power sets will help us to get the basic concepts if sets with examples.
Operations on Sets: Learn the meaning. What are the four basic operations on sets? How the operations are carried out in union of sets and intersection of sets?
Union of Sets: Definition of union of sets with examples. Learn how to find the union of two sets and worked-out examples.
Problems on Union of Sets: Learn how to find the union of two or more sets and worked-out examples of operations on union of sets.
Intersection of Sets: Definition of intersection of sets with examples. Learn how to find the intersection of two sets and worked-out examples.
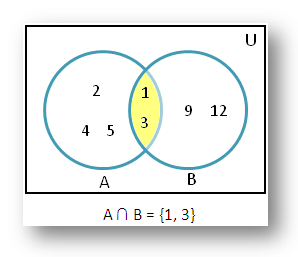
Problems on Intersection of Sets: Learn how to find the intersection of two or more sets and worked-out examples of operations on intersection of sets.
Difference of two Sets: Learn how to find the difference between the two sets and worked-out examples.
Complement of a Set: Definition of complement of a set and their properties with some worked-out examples.
Problems on Complement of a Set: Learn how to find the complement of two or more sets and worked-out examples of operations on complement of sets.
Problems on Operation on Sets: Learn how to find the union and intersection of two or more sets and worked-out examples of the two basic operations of sets.
Cardinal number of a set: Definition of a cardinal number of a set, the symbol used for showing the cardinal number, worked-out examples.
Cardinal Properties of Sets: Learn how to solve the real-life word problems on set using the cardinal properties.
Word Problems on Sets: Apply set operations to solve word problems involving the properties of union and intersection of sets.
Venn Diagrams: Learn to represent the basic concepts of sets using Venn-diagram in different situations.
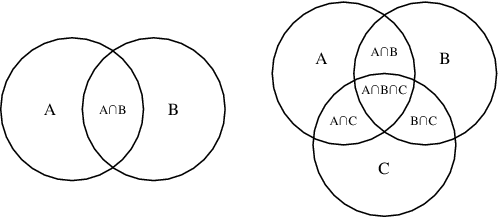
Venn Diagrams in Different Situations: Learn how to use the Venn diagrams in different situations to find the different sets.
Relationship in Sets using Venn Diagram: Learn how to find the relationship of the union, intersection and difference of the two sets using Venn-diagram.
Union of Sets using Venn Diagram: Diagrammatic representation to find the union of two sets and their properties, worked-out examples.
Intersection of Sets using Venn Diagram: Diagrammatic representation to find the intersection of two sets and their properties, worked-out examples.
Disjoint of Sets using Venn Diagram: Learn how to represent the disjoint sets of union and intersection using Venn-Diagram.
Difference of Sets using Venn Diagram: Learn how to represent the difference between two sets using Venn-Diagram.
Symmetric Difference using Venn Diagram: Learn how to represent the symmetric difference between two sets using Venn-Diagram.
Complement of a Set using Venn Diagram: Learn how to find the complement of a sets using Venn-Diagram and their properties.
Examples on Venn Diagram: Learn how to use the basic concepts of sets for solving the different types of problems on Venn diagram.
Laws of Algebra of Sets: Here we will discuss about some fundamental laws of algebra of sets.
Proof of De Morgan’s Law: Learn how to proof De Morgan's Law step-by-step along with the examples.
Properties of Elements in Sets: Learn all the important properties of elements in sets.
Reflexive Relation on Set: What is reflexive relation on set? Learn step-by step to get the reflexive relation in the basic concepts of sets using solved examples.
Symmetric Relation on Set: What is symmetric relation on set? Learn step-by step using solved examples.
Anti-symmetric Relation on Set: What is anti-symmetric relation on set? Learn step-by step using solved examples.
Transitive Relation on Set: What is transitive relation on set? Learn step-by step using solved examples.
Equivalence Relation on Set: What is equivalence relation on set? Learn step-by step to get the equivalence relation in the basic concepts of sets using solved examples.
Exercise
1. Which of the following are sets? Justify your answer.
(a) The collection of all the days in a week beginning with the letter ‘T’.
(b) The collection of all difficult questions in the chapter on sets.
(c) The collection of girls in your class.
(d) The collection of all rivers in India.
(e) The collection of all active teachers in the school.
(f) The collection of all integers more than -3.
(g) The collection of all beautiful flowers in the park.
2. If,
A = {3, 5, 7, 9}
B = {2, 4, 6, 8, 10}
C = {12, 14, 18, 20, 24}
D = {21, 26, 31, 36}
(a) State whether true or false.
(i) 13 ∈ C
(ii) 6 ∉ A
(iii) 9 ∉ A
(iv) 24 ∈ C
(v) 31 ∈ D
(vi) 36 ∉ D
(vii) 20 ∉ C
(viii) 9 ∈ A
(b) Fill in the blanks.
(i) 3 ∈ ___
(ii) 4 ___ B
(iii) 26 ___ C
(iv) 8 ∈ ___
(v) 5 ___ A
(vi) 6 ___ C
(vii) 21 ___ D
(viii) 18 ___ B
3. Write the following sets in the roster form.
(a) A = The set of all even numbers less than 12
(b) B = The set of all prime numbers greater than 1 but less than 29
(c) C = The set of integers lying between -2 and 2
(d) D = The set of letters in the word LOYAL
(e) E = The set of vowels in the word CHOICE
(f) F = The set of all factors of 36
(g) G = {x : x ∈ N, 5 < x < 12}
(h) H = {x : x is a multiple of 3 and x < 21}
(i) I = {x : x is perfect cube 27 < x < 216}
(j) J = {x : x = 5n - 3,n ∈ W, and n < 3}
(k) M = {x : x is a positive integer and x2 < 40}
(l) N = {x : x is a positive integer and is a divisor of 18}
(m) P = {x : x is an integer and x + 1 = 1}
(n) Q = {x : x is a color in the rainbow}
4. Write each of the following in set builder form.
(a) A = {5, 10, 15, 20}
(b) B = {l, 2, 3, 6, 9, 18}
(c) C = {P, R, I, N, C, A, L}
(d) D = {0}
(e) E = { }
(f) F = {0, 1, 2, 3, ......, 19}
(g) G = {—8, —6, —4, —2}
(h) H = {Jan, June, July}
(i) I = {a, e, i, 0, u}
(j) J = {a, b, c, d, …..., z}
(k) K = {1/1, 1/2, 1/3, 1/4, 1/5, 1/6}
(l) L = {1, 3, 5, 7, 9}
5. Write the cardinal number for each of the following.
(a) X = The set of months in a year
(b) Y = The set of letters in the word INTELLIGENT
(c) Z = The set of prime numbers from 2 to 11
(d) P = {x : x is an even prime number}
(e) Q = {x : x is a quadrilateral having 5 sides}
(f) R = {x : x ∈ I, -5 < x < 2}
(g) S = {x | x ∈ W, x + 2 < 9}
(h) T = {x | x is a prime number which is a divisor of 60}
(i) V = {x : x is a 2-digit number such that the sum of digits is 6}
(j) W = The set of hours in a day
6. Classify the following as finite and infinite sets.
(a) A = {x : x ∈ N and x is even}
(b) B = {x : x ∈ N and x is composite}
(c) C = {x : x ∈ N and 3x -2 = 0}
(d) D = {x : x ∈ N and x2 = 9}
(e) E = {The set of numbers which are multiples of 3}
(f) G = {The set of letters in the English alphabet}
(g) H = {The set of persons living in a house}
(h) I = {x | x ∈ I, x < -2}
(i) J = {x | x ∈ P, p is a prime number}
(I) K = The set of fractions with numerator 3.
7. Identify the following as null set or singleton se
(a) A = {x | x ∈ N, 1 < x < 2}
(b) P = {Point of intersection of two lines}
(c) C = {x : x is an even prime number greater than 2}
(d) Q = {x | x is an even prime number}
(e) E = {x : x2 = 9, x is even}
(f) R = {The set of whole numbers lying between 0 and 2}
(g) B = {0}
(h) D = {The set of largest 1 digit number}
(i) F = {The set of triangles having 4 sides}
(j) H = {The set of even numbers not divisible by 2}
8. From the sets given below, select the equal sets.
A = {3, 5, 9, 13}
B = {2, 3, 4, 5}
C = {5, 9, 13, 15}
D = {4, 2, 5, 3}
E = {-2, 2}
F = {o, b}
G = {2, -2}
H = {1, 2}
9. Are two sets A and B equal? Give reasons to support your answer.
(a) A = {x : x is a letter in the word SEAT}
B = {x : x is a letter in the word TASTE}
(b) A = {2, 6, 10, 14}
B = {6, 2, 14, 16}
(c) A = {1, 3, 5, 7, 9}
B = {x : x is a positive odd integer x ≤ 9}
(d) A = {0}
B = {x : x > 15 and x < 5}
10. Which of the following pairs of sets are equivalent or equal?
(a) A = {x : x ∈ N, x ≤ 6}
B = {x : x ∈ W, 1 ≤ x ≤ 6}
(b) P = {The set of letters in the word ‘plane’}
Q = {The set of letters in the word ‘plain’}
(c) X = {The set of colors in the rainbow)
Y = {The set of days in a week}
(d) M = {4, 8, 12, 16}
N = {8, 12, 4, 16}
(e) A = {x | x ∈ N, x ≤ 5}
B = {x | x ∈ I, 5 < x ≤ 10}
Comments
Post a Comment